Probabilidade em Genética

 A probabilidade está presente em diversas situações que envolvem resultados possíveis (espaço amostral) e resultados favoráveis (eventos). Os jogos de azar, como o dado, as cartas e as loterias, necessitam dos cálculos probabilísticos na determinação das chances de um jogador ganhar ou perder. A Genética é outra área que utiliza as teorias da probabilidade, pois os acontecimentos nesse ramo da Biologia envolvem eventos aleatórios, como o encontro dos gametas masculinos e femininos com determinados genes na fecundação. Vamos supor que um indivíduo heterozigoto para determinada característica (Aa) forma dois tipos de espermatozoides, A e a. Caso uma mulher também seja heterozigota, formará óvulos A e a.

 A fecundação ocorrerá ao acaso, pois não sabemos qual espermatozoide, A ou a será responsável pela concepção ou qual célula feminina será fecundada A ou a.

Observe o esquema:

Veja o quadro de possibilidades:

Fundamentos da probabilidade

Probabilidades são medidas matemáticas de possibilidades. Em outras palavras, são uma forma de quantificar (dar um valor numérico específico) o quão provável é um acontecimento. A probabilidade de $1$1 para um evento significa que é garantido que ele vai ocorrer, enquanto a probabilidade de $0$0, significa que seguramente não vai ocorrer. Um exemplo simples é ter 50% ou $1/2$1, slash, 2 das chances de tirar coroa quando você joga uma moeda, como Sal explica neste vídeo introdução a probabilidade.

As probabilidades podem ser empíricas, ou seja, calculadas a partir de observações do mundo real, ou teóricas, ou seja, estimadas usando um conjunto de regras ou pressupostos.

• A probabilidade empírica de um evento é calculada contando-se o número de vezes que o evento ocorreu e dividindo esse valor pelo número total de vezes que o evento poderia ter ocorrido. Por exemplo, se o evento que você está buscando fosse o de uma ervilha com semente rugosa e você a viu $1{.}850$1, point, 850 vezes de um total de $7{.}324$7, point, 324 sementes examinadas, a probabilidade empírica de se ter uma ervilha de semente rugosa seria de $1{.}850/7{.}324 = 0{,}253$1, point, 850, slash, 7, point, 324, equals, 0, comma, 253, ou muito perto de $1$1 em $4$4 sementes.
• A probabilidade teórica de um evento, por sua vez, é calculada com base em informações sobre as regras e circunstâncias que produzem o evento. Esse tipo de probabilidade reflete o número de vezes que espera-se que um evento ocorra em relação ao número de vezes que ele poderia ocorrer. Por exemplo, se você tivesse uma planta de ervilha heterozigota para o gene da forma da semente (Rr) e a deixasse realizar autofecundação, você poderia usar as regras da probabilidade e seu conhecimento de genética para prever que $1$1 de cada $4$4 descendentes teria dois genes recessivos (rr) e seria rugosa, correspondendo a $0{,}25$0, comma, 25 ($1/4$1, slash, 4) de probabilidade. Vamos discutir mais sobre como aplicar as regras da probabilidade neste caso.

Em geral, quanto maior for o número de dados usados para calcular uma probabilidade empírica, tais como formas de sementes individuais de ervilha, tanto mais próximo da probabilidade teórica esse número vai chegar.

Para que Mendel pudesse chegar aos seus resultados, ele utilizou muitos métodos estatísticos para sua interpretação, calculando as probabilidades de ocorrer os eventos. A probabilidade serve para estimar matematicamente a possibilidade de ocorrer eventos que acontecem ao acaso, ou seja, por questão de sorte. Pode ser definida pela seguinte fórmula:

P(A)=AS

Onde P é a probabilidade de um evento ocorrer, A é o número de eventos desejados e S é o número total de eventos possíveis.

Exemplo: Quando jogamos uma moeda para cima, temos duas possibilidades de resultado: ela cair com a face “cara” voltada para cima, ou com a face “coroa” voltada para cima. Portanto temos duas possibilidades. A possibilidade de sair cara é de 1/2 ou 50%, pois temos uma chance (sair cara) em duas possibilidades (cara ou coroa).

assim como

A probabilidade é um evento esperado, uma possibilidade, portanto, não é certeza que vá ocorrer. Quanto mais repetições ocorrerem, mais chances a previsões terão de dar certo.

Quando utilizamos cálculos de probabilidades em genética, não podemos dizer que os indivíduos que irão nascer terão obrigatoriamente os genótipos calculados, pois é questão de sorte. Quanto mais indivíduos nascerem, mais chances dos resultados práticos se aproximarem dos cálculos.

Regra do “e”

Quando a ocorrência de um evento não afeta a ocorrência do evento seguinte, dizemos que eles são independentes. Quando queremos calcular a probabilidade da ocorrência de eventos independentes de uma vez só, utilizamos a regra do “e”.

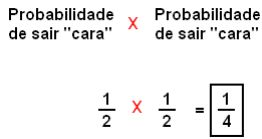
Exemplo: Se jogarmos duas moedas para cima, qual a probabilidade de sair “cara” nas duas?

Resolução:
O fato de sair “cara” em uma moeda não afeta a chance de sair “cara” na outra. Quando acontece esse tipo de evento, multiplicamos as probabilidades dos eventos independentes:

R = 1/4 ou 25%

Em genética utilizamos a mesma linha de raciocínio. Por exemplo: Qual a probabilidade de um casal ter dois filhos do sexo feminino?

Resolução: O nascimento da primeira filha não afeta a chance de o segundo filho ser do sexo feminino, pois a segregação dos alelos de um gene é tão ao acaso quanto jogar uma moeda para cima e obter “cara” ou “coroa”. Portanto:

R = 1/4 ou 25%

Regra do “ou”

A regra do “ou” é utilizada quando queremos calcular a probabilidade de ocorrer um evento ou outro numa mesma oportunidade.
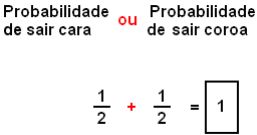
Por exemplo: Qual a chance de sair “cara” ou “coroa” em uma jogada de moeda?

Resolução: Esses dois eventos não ocorrem juntos, pois é um ou o outro, logo são mutuamente exclusivos. Quando temos esse tipo de situação, somamos as duas probabilidades: